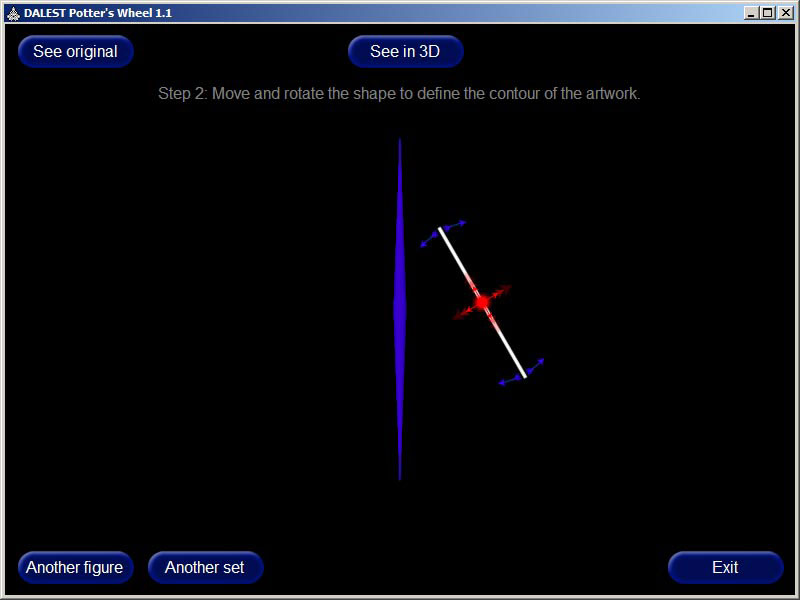
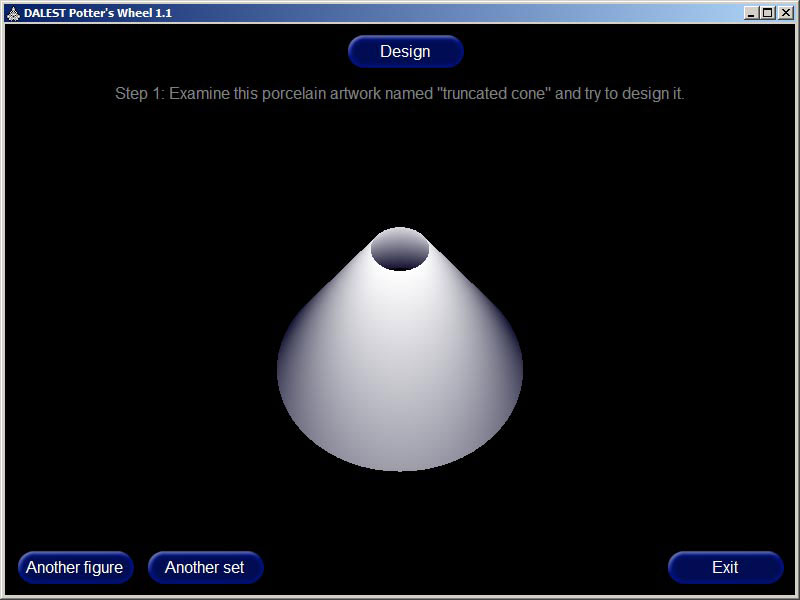
The Potter's Wheel is aDALESTapplication. The main idea in the is this: the user has a simple object (a segment, a circle, a square, a triangle or a sinuidal curve) which can be moved and rotated. There is an axis on the screen and the object is positioned on the left, on the right or across that axis. When the user is ready, the application rotates the object around the axis and produces a 3D rotational image – this process is similar to how potters use clay and a wheel to make pottery. The trick is that the object orientation relative to the axis is important. Small changes can cause interesting differences

There are over 80 objects which can be constructed using only the 5 objects above (one at a time). They are provided as problems grouped in 5 sets (one set for each 2D figure). In the last version of the application a new figure is added – a free transformable curve together with 25 new examples. When transformig the curve the user has 5 base points – each point can be moved and turned. Turning points affects tangents of the curve, because is a chain of Bezier curves

1. Try to reconstruct a given 3D object by using the provided 2D figure
2. Study the various figures produces by a segment. What are their names and properties?
3. Study the various figures produced by a circle. Do these figures have geometrical names?
4. Study the various figures produced by a triangle. Which of them can be produced by a segment? Can you find all 3D solids which have geometrical names?
5. Study the various figures produced by a square. Which of them can be produced by a segment? By a triangle? By two triangles?
6. Study the various figures produced by a sine curve. Which of them could be reproduced by a cosine cuve?
7. Find the role of the axis; investigate the case when the object crosses the axis
8. Try to find out a 3D solid which can be produced by a shape entirely to the left of the axis, but cannot be produced by the same shape entirely to the right of the axis; if not possible, then prove it
9. Examine the split mode (especially when using the sine curve) and explain what a rotational object has such appearance
10. Create you own sets and problems and give them to others to solve
11. Can you find rotational objects around you, in your home, or out in the street? Create models of these objects; create your own library of rotational objects
12. Try to describe a rotational object with words, so that another person can rebuild it
13. Play with the free-form curve and try to model various objects from your everyday life
14. Create puzzles with the free-form curve and let others solve them